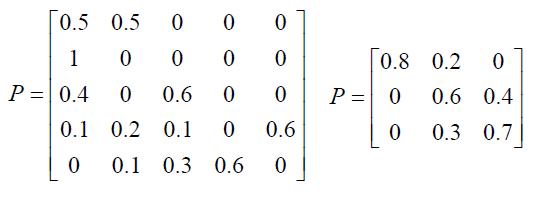Clasificación de estados de una Cadena de Markov
Para la clasificación de estados de una Cadena de Markov en tiempo discreto utilizaremos 2 ejemplos:
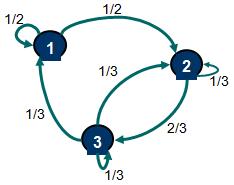
Ejemplo 1:
Ejemplo 2:
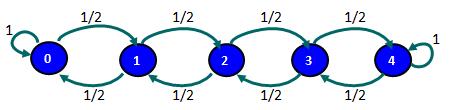
Si existe una probabilidad no nula que comenzando en un estado i se pueda llegar a un estado j al cabo de un cierto número de etapas (digamos n) se afirma que el estado j es accesible desde el estado i. Si consideramos el ejemplo 1 podemos afirmar que el estado 3 es accesible desde el estado 1. Aún cuando en una etapa no podemos llegar desde el estado 1 al estado 3, si podemos hacerlo al cabo de 2, 3, ..., n etapas. Cabe destacar en este punto que es relevante que exista una probabilidad no nula que comenzando en 1 se pueda llegar a 3 al cabo de un cierto número de etapas no importando el valor exacto de esta probabilidad para un n cualquiera. En cuanto al ejemplo 2, se puede verificar que el estado 2 es accesible desde el estado 3, sin embargo, el estado 2 no es accesible desde el estado 4 (esto porque una vez que se llega al estado 4 no se sale de ese estado). Finalmente, dos estados que son accesibles viceversa se dice que se comunican y que pertenecen a una misma clase de estados.
Una Cadena de Markov donde todos sus estados son accesibles entre sí y por tanto se comunican se dice que es irreducible, es decir, que existe una única clase de estados. Este es el caso del ejemplo 1.
En cambio si al menos existen 2 clases de estados la cadena ya no es irreducible. Si tenemos 2 estados que no se comunican (esto porque no son accesibles viceversa) estos estados perteneceran a distintas clases de estados. En el ejemplo 2 existen 3 clases de estados {0}, {1,2,3}, {4} (en consecuencia no es una cadena irreducible). En cuanto al estado 0 y estado 4, estos son estados absorventes debido a que una vez que se accede a ellos la probabilidad de seguir en ese estado es de un 100%. Un estado absorvente define una clase de estados por si mismo.
Una definición adicional es la periodicidad de un estado. Un estado se dice que tiene periodo d, para el mayor valor entero de d que cumpla:
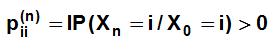
sólo para valores de n pertenecientes al conjunto {d, 2d, 3d, ....}. Si d=1 decimos que el estado es aperiódico. En otras palabras, un estado es periódico si, partiendo de ese estado, sólo es posible volver a él en un número de etapas que sea múltiplo de un cierto número entero mayor que uno
En el ejemplo 1 todos los estados son aperiódicos. En el ejemplo 2 los estados 1, 2 y 3 son periódicos con periodo d=2, es decir, que comenzando, por ejemplo, en el estado 1, la probabilidad de volver al mismo estado es sólo no nula para una cierta cantidad de pasos o etapas múltiplo de 2.
Un estado es recurrente en la medida que comenzando en él se tenga la certeza de volver en algun momento del tiempo (una determinada cantidad de etapas) sobre si mismo. Alternativamente, un estado es transciente si no se tiene la certeza de volver sobre si mismo. En el ejemplo 1 todos los estados son recurrentes. En el ejemplo 2 los estados 1, 2 y 3 son transcientes debido a que si se comienza en cualquiera de ellos no se puede asegurar con certeza que se volverá al mismo estado en algún momento (esto debido a que existe una probabilidad no nula de acceder a un estado absorvente: 0 o 4). Los estados absorventes por definición son estados recurrentes.
Si tenemos una Cadena de Markov que tiene una cantidad finita de estados e identificamos un estado recurrente, este será recurrente positivo. Si la cantidad de estados es infinito entonces un estado recurrente será recurrente nulo.
Ejercicios propuestos clasificación de estados de una Cadena de Markov en Tiempo Discreto
Considere las siguientes matrices de probabilidades de transición para una Cadena de Markov en tiempo discreto. Determine si la cadena es irreducible o no determinando la clase de estados. Verifique si los estados son recurrentes o transcientes y determine si son periódicos o aperiódicos.