Algoritmo de Branch and Bound
El método de Branch and Bound (en español Ramificación y Acotamiento) aborda la resolución de modelos de programación entera a través de la resolución de una secuencia de modelos de programación lineal que consituirán los nodos o subproblemas del problema entero. Si bien el procedimiento es extendible a un número mayor de variables, para efectos prácticos ilustraremos su aplicación para modelos de programación entera en 2 variables.
Ejemplo Branch and Bound
Resuelva el siguiente modelo de programación entera a través del algoritmo de ramificación y acotamiento (Branch and Bound)
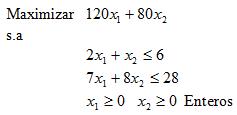
El primer paso consiste en resolver el problema sin considerar las condiciones de integralidad, es decir, asumiendo que es un modelo de Programación Lineal. El siguiente gráfico muestra la resolución gráfica donde el área en verde corresponde al dominio de soluciones factibles asociado al problema lineal lo que se denomina la relajación continua del problema entero. Adicionalmente, sólo con el objetivo de ilustrar se han marcado con azul las posibles soluciones enteras para este problema. En este sentido resulta evidente que el dominio de soluciones factibles del problema entero es un subconjunto del dominio del problema lineal y esto en el caso de un problema de maximización determina que el valor óptimo del problema lineal será una cota superior del valor óptimo del problema entero.
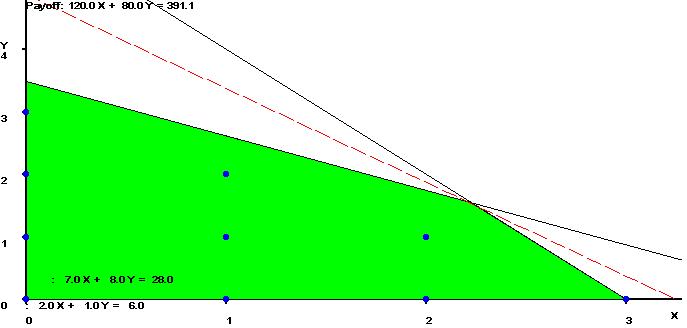
La relajación continua (Problema P0) nos da como solución óptima X1=20/9 y X2=14/9 con valor óptimo V(P0)=319,1. Dado que al menos una variable de decisión toma valor fraccionario se debe buscar una aproximación a valor entero. En este caso en particular con 2 soluciones fraccionarias como criterio se puede seleccionar aquella con un mayor impacto (coeficiente) en la función objetivo, sin embargo, no importando cuál de ellas se seleccione en un inicio los resultados serán los mismos.
En consecuencia, seleccionaremos X1 y aproximaremos los resultados (20/9=2,222) al entero superior e inferior más cercano. Esto genera 2 subproblemas que llamaremos P1 y P2 respectivamente. El problema P1 es similar a P0 pero considera como restricción adicional X1<=2. Al resolver dicho problema se obtiene X1=2 y X2=7/4 con V(P1)=380. El problema P2 es similar a P0 pero adicionalmente tiene la restricción X1>=3, con solución óptima X1=3 y X2=0 y V(P2)=360. Este nodo (P2) se agota y sólo el P1 puede generar nuevos nodos.
Cabe destacar que un nodo o subproblema se agota en las siguientes situaciones: 1) Se alcanza una solución entera, 2) El problema es infactible, 3) Se obtiene una solución fraccionaria pero no es necesario continuar dado que ésta no es mejor (en términos de valor de la función objetivo) que una solución entera que se ha alcanzado previamente.
Continuando con el procedimiento el P1 genera 2 nuevos nodos. P11 (similar a P1 con la restricción adicional X2<=1) con solución X1=2 y X2=1 y V(P11)=320. El problema P12 (similar a P1 con la restricción adicional X2>=2) con solución X1=12/7 y X2=2 y V(P12)=365,7.
Sólo P12 genera nuevos nodos: P121 (similar a P12 con la restricción adicional X1<=1) con solución X1=1 y X2=21/8 y V(P121)=330. Adicionalmente el problema P122 (similar a P12 con la restricción adicional X1>=2) resulta ser infactible al no existir solución.
Finalmente, si bien se puede continuar ramificando (generando nodos) a contar del problema P121 esto no es necesario dado que el valor óptimo sólo podrá ir disminuyendo (dado que cada vez se resuelve un problema sobre un dominio de soluciones factibles menor) y por tanto en ningún caso se podrá obtener una solución entera mejor que la que ya se dispone (P2). Por tanto X1=3 y X2=0 es solución óptima del problema entero con valor óptimo V(PE)=360. Se recomienda verificar que se obtienen los mismos resultados ramificando inicialmente por X2 en vez de X1.