Método Simplex Dual
El método simplex dual resulta ser una estrategia algoritmica eficiente cuando luego de llevar un modelo de programación lineal a su forma estándar, la aplicación del método simplex no es inmediata o más bien compleja, por ejemplo, puede requerir la utilización del método simplex de 2 fases.
Una aplicación típica del método simplex dual es en la resolución de problemas con una función objetivo de minimización, con restricciones del tipo mayor o igual y donde las variables de decisión son mayores o iguales a cero.
Ejemplo Simplex Dual
Considere el siguiente modelo de Programación Lineal:
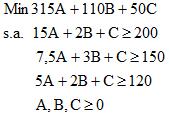
Paso 1: Se lleva el modelo a su forma estándar. En nuestro ejemplo esto se logra agregando variables de exceso en cada una de las restricciones (3 primeras: S1, S2, S3, respectivamente). Luego, se multiplica cada fila de las restricciones por -1 de modo de disponer una solución básica inicial (infactible) en las variables de exceso S1, S2 y S3. De esta forma se obtiene la siguiente tabla inicial.
A |
B |
C |
S1 |
S2 |
S3 |
|
-15 |
-2 |
-1 |
1 |
0 |
0 |
-200 |
-7,5 |
-3 |
-1 |
0 |
1 |
0 |
-150 |
-5 |
-2 |
-1 |
0 |
0 |
1 |
-120 |
315 |
110 |
50 |
0 |
0 |
0 |
0 |
Paso 2: Se selecciona el lado derecho "más negativo" lo cual indicará cuál de las actuales variables básicas deberá abandonar la base. En el ejemplo el lado derecho más negativo se encuentra en la primera fila, por tanto S1 deja la base. Para determinar cual de las actuales variables no básicas (A, B, C) entrará a la base se busca el mínimo de {-Yj/aij} donde aij es el coeficiente de la respectiva variable no básica en la fija i (del lado derecho más negativo, marcado en verde) y donde Yj es el costo reducido de la respectiva variable no básica. De esta forma se obtiene: Min {-315/-15, -110/-2, -50/-1} = 21, donde el pivote (marcado en rojo) se encuentra al hacer el primer cuociente, por tanto A entra a la base.
Paso 3: Se actualiza la tabla anterior siguiendo un procedimiento similar al utilizado en el Método Simplex. En el ejemplo se debe dejar a la variable A como básica y S1 como no básica. La tabla que resulta es la siguiente:
A |
B |
C |
S1 |
S2 |
S3 |
|
1 |
2/15 |
1/15 |
-1/15 |
0 |
0 |
40/3 |
0 |
-2 |
-1/2 |
-1/2 |
1 |
0 |
-50 |
0 |
-4/3 |
-2/3 |
-1/3 |
0 |
1 |
-160/3 |
0 |
68 |
29 |
21 |
0 |
0 |
-4.200 |
Paso 4: Continuar las iteraciones y siguiendo el mismo procedimiento hasta disponer de una solución básica factible. Luego de unas iteraciones se obtiene la siguiente tabla final:
A |
B |
C |
S1 |
S2 |
S3 |
|
1 |
0 |
0 |
-1/10 |
0 |
1/10 |
8 |
0 |
1 |
0 |
1/4 |
-1 |
3/4 |
10 |
0 |
0 |
1 |
0 |
2 |
-3 |
60 |
0 |
0 |
0 |
4 |
10 |
36 |
-6.620 |
La solución óptima es A=8, B=10, C=60 (marcado en verde) con valor óptimo V(P)=6.620 (marcado en rojo - se obtiene con signo cambiado). También es interesante notar que los costos reducidos de las variables artificiales S1, S2 y S3 (marcado en amarillo), corresponde a la solución óptima del modelo presentado en el tutorial de solver, esto dado que dicho modelo resulta ser el problema dual de nuestro ejemplo.
¿PROBLEMAS CON SIMPLEX DUAL?: Ingrese a la aplicación del Método Simplex la cual también le permitirá resolver modelos de Programación Lineal utilizando esta metodología.