Dualidad en Programación Lineal
Consideremos nuevamente el ejemplo utilizado para presentar el tutorial de Solver:
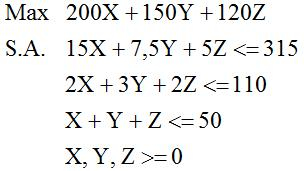
Supongamos que deseamos conocer una cota superior del valor óptimo de este problema sin la necesidad de resolver dicho problema. Por ejemplo, si multiplicamos la restricción 3 por 200 obtenemos: 200X + 200Y + 200Z <= 10.000. Claramente el lado izquierdo de esta restricción amplificada es mayor o igual a la expresión que define la función objetivo, por tanto podemos afimar que el valor óptimo de este problema es menor o igual a 10.000 ( V(P)<=10.000 ). Por supuesto se puede buscar otras combinaciones de modo de definir una mejor cota superior a la que se utiliza como ejemplo.
En este sentido si consideramos A, B y C como multiplicadores asociados a cada una de las restricciones, la forma de encontrar la mejor cota superior para el problema original (que llamaremos en adelante Primal) se obtiene resolviendo el siguiente problema (denominado Dual):
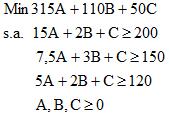
Este problema puede ser resuelto a través del método simplex dual como se explica en detalle en dicha sección. Se obtiene de esta forma la siguiente solución óptima: A=8, B=10, C=60, con valor óptimo de 6.620. Si multiplicamos las restricciones del problema dual por estos multiplicadores logramos la mejor cota superior:
8(15X + 7,5Y + 5Z) + 10(2X + 3Y + 2Z) + 60(X + Y + Z) <= 8*315 + 10*110 + 60*50
200X + 150Y + 120Z <= 6.620
Se puede verificar adicionalmente que el precio sombra de las respectivas restricciones del problema primal (ver informe de sensibilidad en la sección de solver de excel) corresponde a las variables duales óptimas o solución óptima del problema dual, con valor óptimo equivalente.
En general las relaciones de dualidad se pueden resumir en la siguiente tabla:
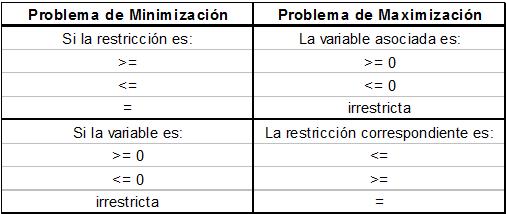
Teoremas de Dualidad
La dualidad en programación lineal provee de resultados teóricos interesantes que justifican su uso como herramienta alternativa y complementaria de resolución.
TEOREMA DE DUALIDAD DÉBIL: En general, el valor de cualquier solución factible del problema de minimización, provee una cota superior del valor óptimo del problema de maximización. Análogamente, el valor de la función objetivo de cualquier solución factible del problema de maximización es una cota inferior del valor óptimo del problema de minimización.
TEOREMA DE DUALIDAD FUERTE: En el óptimo el valor de la función objetivo del problema primal será igual al valor de la función objetivo del problema dual evaluada en la solución dual óptima. Si el problema primal es no acotado, entonces el dual es infactible. Alternativamente si el problema primal es infactible, entonces el dual es no acotado.
TEOREMA DE HOLGURAS COMPLEMENTARIAS:Una variable en el primal esta asociada a una restricción en el dual (y viceversa). En este sentido si en el primal existe una variable no básica (valor igual a cero), en el dual la restricción asociado no está activa, es decir, no se cumple en igualdad. Análogamente, si la variable es básica en el primal, la restricción asociada en el dual se cumple en igualdad. Este resultado teórico es útil toda vez que simplifica la forma de obtener la solución óptima dado que como en un problema lineal la solución óptima (en caso de existir) esta en un vértice, esto implica resolver un sistema de ecuaciones (con restricciones de igualdad).