Cadenas de Markov
Un proceso estocástico en tiempo discreto es una Cadena de Markov en la medida que se verifiquen las siguientes propiedades:
Propiedad Markoviana:
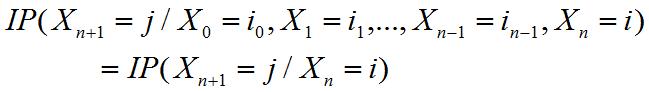
Donde i0, i1, ..., in-1, i, j son posibles “ estados” o valores que puede tomar el proceso estocástico en las distintas etapas. Esto consiste básicamente en afirmar que el futuro (t=n+1) es independiente del pasado dado el presente (t=n).
Propiedad Estacionaria: La probabilidad
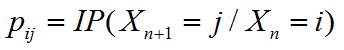
No depende de la etapa n. Por ejemplo, la probabilidad de pasar del estado i al estado j será siempre la misma no importando el número de la etapa.
Si consideramos que la variable aleatoria asociado a este proceso markoviano toma un número finito de estados (digamos M) las probabilidades de transición de un estado a otro se pueden resumir en una matriz P denominada matriz de transición de probabilidades en una etapa. Adicionalmente si conocemos la distribución de probabilidad para la etapa inicial (que denotamos por f0) estamos en condiciones de conocer el proceso estocástico, que consiste en determinar la distribución de probabilidad en cada etapa.
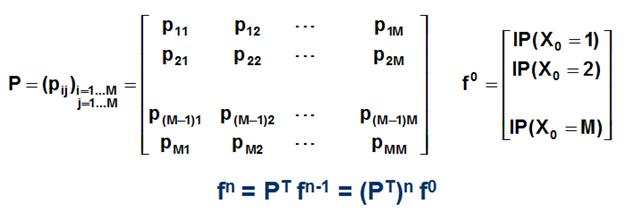
Ejemplo Cadena de Markov en Tiempo Discreto
Suponga que en un juego existen 2 jugadores, cada uno de los cuales dispone inicialmente de 2 monedas. En cada jugada se gana una moneda con probabilidad ½ o se pierde una moneda con probabilidad ½. El juego termina cuando un jugador tiene 4 monedas o se queda con ninguna. Modele como una Cadena de Markov la situación descrita.
Desarrollo: El primer caso consiste en identificar la variable aleatoria la cuál debe representar el problema planteado, en este caso la evolución del juego al cabo de cada etapa o jugada. Se define la variable aleatoria en tiempo discreto Xn : Cantidad de monedas que tiene uno de los jugadores (digamos el jugador A) al cabo de la enésima jugada.
Luego se debe identificar los posibles valores o estados que puede tomar esta variable aleatoria para una etapa n cualquiera. Sabemos que el jugador A comienza el juego con 2 monedas y el juego termina cuando pierde todo (y por tanto el jugador B gana) o cuando gana todo (y por tanto el jugador B pierde). En consecuencia, los valores posibles para Xn son {0,1,2,3,4}.
A continuación se debe determinar las probabilidades de transición (en una etapa). Por ejemplo, si actualmente el jugador A tiene 2 monedas, la probabilidad que tenga 3 monedas al cabo de una jugada es ½ (probabilidad de ganar) y la probabilidad de que tenga 1 moneda es ½ (probabilidad de perder). De esta forma se identifican las distintas combinaciones o probabilidades de que comenzando en un estado "i" se pueda pasar a un estado "j" al cabo de una etapa. Notar que si el jugador A tiene 0 monedas la probabilidad que continue en ese estado es 1 (o 100%) dado que no tiene monedas para seguir jugando. De la misma forma si el jugador A tiene 4 monedas el jugador B tiene 0 y por tanto la probabilidad de que el jugador A se mantenga en ese estado es de 1 (o 100%).
Las probabilidades de transición en una etapa se pueden representar haciendo uso de un grafo o en forma resumida a través de la matriz de transición de probabilidades.
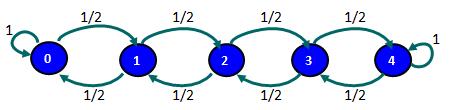
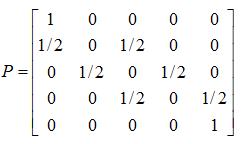
Cabe destacar que la suma de las probabilidades para cada fila en la matriz de transición P es de un 100%.
Podemos responder preguntas adicionales cómo por ejemplo ¿Cuál es la probabilidad de que el jugador A tenga 2 monedas al cabo de 2 jugadas?
Haciendo uso del grafo y dado que actualmente el jugador A tiene 2 monedas, se busca identificar las combinaciones que permitan a este jugador mantener esta cantidad de monedas al cabo de 2 etapas. Esto se logra ganando la próxima jugada (con probabilidad ½) y perdiendo la jugada que sigue (con probabilidad ½). También se llega al mismo resultado perdiendo la próxima jugada pero luego ganando en la jugada que sigue. Por tanto la probabilidad de tener 2 monedas al cabo de 2 etapas es P(X2=2/X0=2) = ½*½ + ½*½ = ½.